线性回归1

一、任务驱动

简单来讲，我们要使用线性回归的方法，求出一个函数，将如图14个参数输入进去后，得到预测房价。

示意图

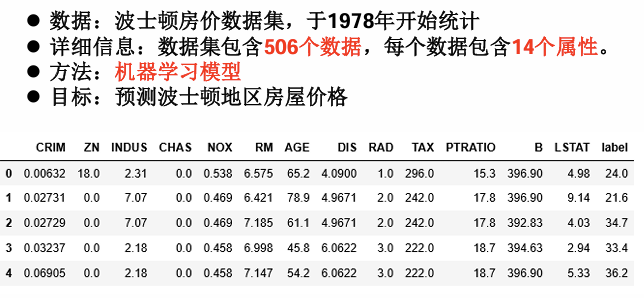
二、线性回归是什么？

线性回归，即要求所有点到某线的距离之和最小，一般是看均方和，如图中所示。

线性回归

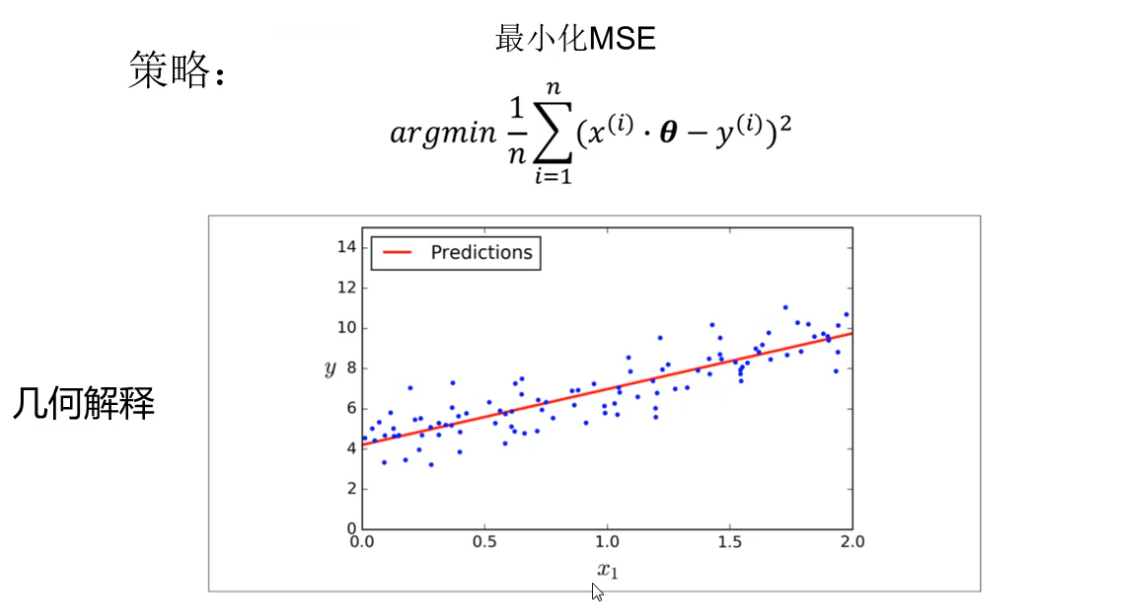
用矩阵表达如图所示。

用矩阵表达

三、如何算出参数θ？

1. 也就是多元二次函数最小值问题，举个例子，当“θx”为一元，则直接对（θx-y）²求导，让导数为零即可。
   但这种方法有限制：
   • 矩阵的维度无法太大。
   • 速度会变慢。
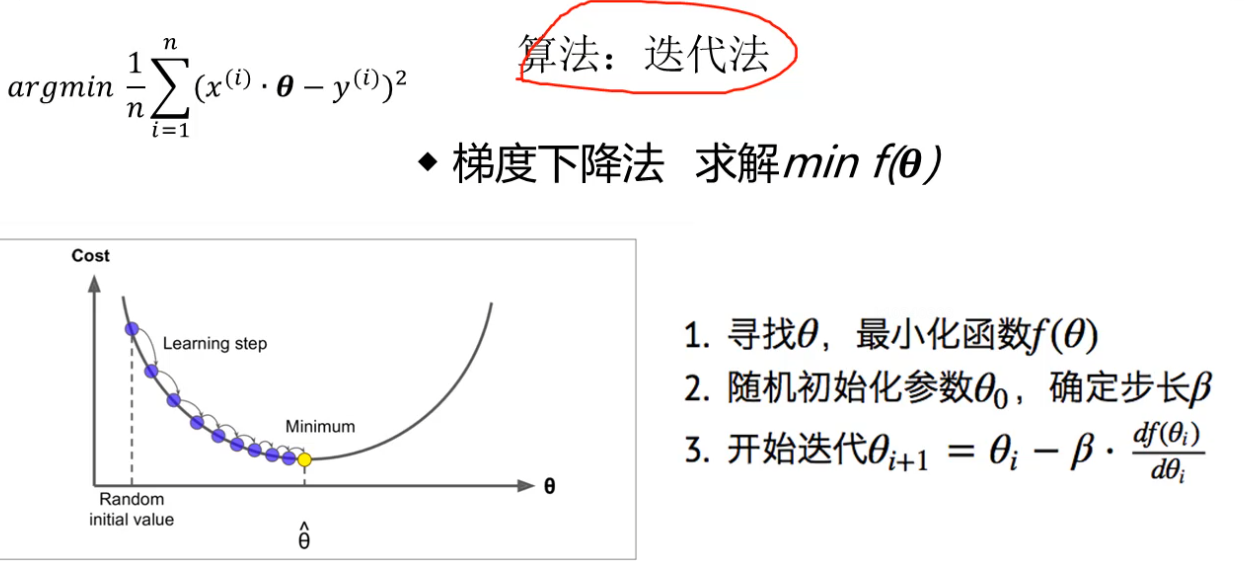
2. 梯度下降法，推荐。
   如图。
   

   图解梯度下降法
3. 梯度下降法注意事项
   3.1 步长β：也称为学习效率，属于超参数。要大小合适，或者前期较大，后期较小。若太大，结果反复横跳，若太小，耗时太长。
   3.2 下凸函数（如x²），唯一极小值即为最小值，要小心上凸函数以及局部平缓的情况，可能会陷入局部最优（极小值、鞍点）。可以取多个初始值。
   3.3 注意去量纲，进行标准化与归一化。